A world without mosquitos

Breaking Mendel’s rules

By default, genes have a 50% chance to be passed on from parent to offspring, since each individual has 2 copies of a gene and only one copy can be passed on to the next generation per parent. However, a number of tricks exist to rig this coinflip and make sure a particular copy is passed on. Genes that are not 50 but 100% sure to be transferred to offspring can spread in a population even when they make the individuals that carry them less healthy. The researchers used one of these tricks to boost the spread of a gene that can cause entire populations to collapse. The key to this gene’s potency is that it only starts affecting the population once it is already quite common in the gene pool. Only females that get an infected copy from both parents are struck with infertility, males and females with only a single infected copy are completely unaffected. However, thanks to the researchers trick, these infected individuals are sure to pass on the gene to their offspring. This allows the gene to spread exponentially in the population until it is too late. At a certain tipping point most individuals carry at least one copy of the gene and suddenly the next generation is in real trouble. Almost all of the offspring get a copy of the tampered gene from both parents and most females turn out infertile. One generation later the process repeats and complete extinction is suddenly a real possibility.

I found this idea to be intriguing and decided to create a simple object-oriented population dynamics model to see if I could replicate this phenomenon and learn something along the way.

Building a population model

I prefer building object-oriented population models over purely mathematical ones as they remain intuitive even when you add layers of complexity. In our mosquito population model, the lowest level is simply a mosquito object that holds the relevant details for an individual, being its sex and the genes it carries. Each individual has two copies of our gene of interest. I define the status of the gene as ‘infected’ (True) or not infected (False). While the term ‘infected’ is not technically correct I’ll keep using this analogy in this post for the sake of explainability.

class Mosquito:
    """Contains the details of each Mosquito"""
    def __init__(self, mother_gene_infected, father_gene_infected, sex):
        # The infection status of each gene is either True or False
        self.genes = [mother_gene_infected, father_gene_infected]
        self.sex = sex

The main body of code goes into our Simulation class. When an object of this class is created we have to pass it a number of healthy and infected mosquitos to make up the population. I always used 10.000 healthy Mosquitos and introduced a varying number of infected ones. Once the Simulation object is created we can use it’s main_loop method to run the simulation for a number of generations. Each generation the population will go through 2 steps: density-dependent survival and reproduction. In the density-dependent survival step most of the population will be decimated to simulate the fact that most individuals that are born don’t get to create new offspring themselves, mosquito life is hard too. I set the density regulation function’s parameters to allow a stable population of about 10.000 individuals. When the population gets bigger than that (high density), survival chances will go down and when it is smaller, survival chances will be better and allow the population to grow. This process mimics competition between Mosquitos for some limited resource that they need, like ponds to lay their eggs in, or sleeping humans to bite.
In the reproduction step the surviving females will select a random mate from the male population and create about 100 new individuals. Note that females with two copies of the malicious gene are infertile and thus are excluded from the reproduction process. The newborn individuals get a gene from both their mother and father. When a parent carries a copy of the malicious gene they will always pass it on to the offspring due to the researcher’s hack of Mendel’s law.

import numpy as np
class Simulation:
    """Regulates the population and simulation"""
    def __init__(self, n_healthy, n_infected):
        """
        Create a population (list of individuals)
        with a number of healthy and infected individuals
        """
        # The construct ['Male', 'Female'][x % 2] will make
        # sure that we produce mosquitos of alternating sex,
        # resulting in a 0.5 sex ratio
        self.pop = [Mosquito(mother_gene_infected=False,
                             father_gene_infected=False,
                             sex=['Male', 'Female'][x % 2])
                    for x in range(n_healthy)]
        self.pop.extend([Mosquito(mother_gene_infected=True,
                                  father_gene_infected=False,
                                  sex=['Male', 'Female'][x % 2])
                         for x in range(n_infected)])

    def reproduction(self):
        """
        Replace the old population by a new one
        """
        # Divide the population into females and males.
        # Females with 2 copies of the infected gene are
        # infertile and not selected
        females = [m for m in self.pop if (m.sex == 'Female')
                   and (sum(m.genes) < 2)]
        males = [m for m in self.pop if m.sex == 'Male']

        # The old population is overwritten by an empty list
        # and will be filled with new individuals
        self.pop = []
        # If there is at least one fertile female..
        if females:
            # select a random male mate for each female
            mates = np.random.choice(males, len(females))
            for i, f in enumerate(females):
                # Pass on genes to about 100 offspring
                # (sample from Poisson distribution)
                # Since gene drive is in place,
                # an infected gene will always be passed on.
                # The construct ['Male', 'Female'][x % 2]
                # will make sure that we produce mosquitos of
                # alternating sex, resulting in a 0.5 sex ratio
                self.pop.extend(
                    [Mosquito(mother_gene_infected=sum(f.genes) > 0,
                              father_gene_infected=sum(mates[i].genes)>0,
                              sex=['Male', 'Female'][n % 2])
                     for n in range(np.random.poisson(100))])

    def density_dependent_survival(self, a=0.25, beta=0.5):
        """
        Reduce the current population in a density-dependent manner.
        When the population is big the survival rate is lower
        than when the population is low.
        Surviving individuals will go on to reproduce
        """
        # Single species density regulation based on Hassell & Comins
        survival_rate = (1 + a * len(self.pop)) ** -beta
        n_survivors = int(len(self.pop) * survival_rate)

        # if there are survivors we select them randomly
        # from the current population
        if n_survivors:
            np.random.shuffle(self.pop)
            self.pop = self.pop[0:(n_survivors + 1)]
        else:
            self.pop = []

    def population_statistics(self):
        """
        Calculate the population statistics we'll plot
        """
        # Count the number of infected individuals
        infected = len([m for m in self.pop if (sum(m.genes) > 0)])
        # Count the number of double infected (homozygote) individuals
        double_infected = len([m for m in self.pop if (sum(m.genes)==2)])
        return [len(self.pop), infected, double_infected]

    def main_loop(self, n_generations):
        """
        The main loop function of a single simulation
        Each iteration is a generation
        """
        # create an array to store per-generation results
        results_array = np.zeros(shape=(n_generations + 1, 3))
        # add the statistics of the initial population
        results_array[0] = self.population_statistics()

        for n in range(n_generations):
            self.density_dependent_survival()
            self.reproduction()
            results_array[n + 1] = self.population_statistics()

        # return the per-generation evolution of the infection
        # and whether the population went extinct
        return results_array, len(self.pop) == 0

To plot the results of our model we’re going to need some visualization functions. These are included below for completeness.

import pylab
import matplotlib.pyplot as plt

def plot_meta_results(results):
    """Results plotter for results over multiple simulations"""
    # switch from proportions to percentages and plot
    plt.plot(100 * results[:, 0], 100 * results[:, 1])
    plt.xlabel('Population % of infected individuals introduced')
    plt.ylabel('% of simulations with extinction')
    plt.show()

def plot_simulation_results(results):
    """Results plotter for results of single simulation"""
    x = np.linspace(0, len(results) - 1, len(results))
    popsize = results[:, 0]
    all_infected = results[:, 1]
    double_infected = results[:, 2]

    pylab.plot(x, popsize, '-b', label='Population')
    pylab.plot(x, all_infected, '-r', label='All infected')
    pylab.plot(x, double_infected, '-g', label='Double infected')
    pylab.legend(loc='lower right')
    pylab.xlabel('Generation')
    pylab.ylabel('Number of individuals')
    pylab.ylim(0, max(popsize) * 1.1)
    pylab.show()

Simulating a Mosquito’s worst nightmare

Now that we’ve built our simple abstraction of a Mosquito population we can start playing around. Let’s introduce 100 infected mosquitos carrying one copy of the malicious gene each into a population of 10.000 healthy mosquitos.

if __name__ == '__main__':
    # -------------------
    # simulation settings
    # -------------------
    # While there is randomness in our simulation,
    # for a particular random seed the outcome will be the same.
    np.random.seed(1)
    # Number of uninfected mosquitos present in the 1st generation
    n_healthy_mosquitos = 10000
    n_infected_mosquitos = 100
    dyn = Simulation(n_healthy=n_healthy_mosquitos,
                     n_infected=n_infected_mosquitos)

    # a single run of the simulation
    results = dyn.main_loop(n_generations=20)[0]
    plot_simulation_results(results)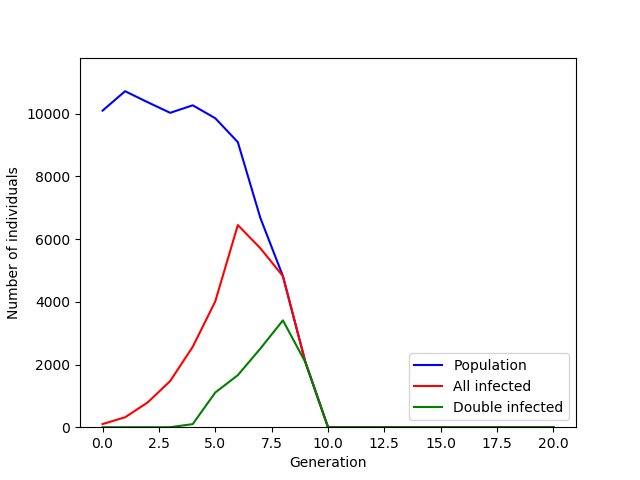

The number of infected mosquitos (red line) increases exponentially and then in a few generations crashes along with the rest of the population. In the 8th generation, all individuals are infected with at least 1 copy of the gene which means that in the 9th and final generation all individuals carry 2 copies of the gene (green line), ruling out the existence of fertile females.

How many infected Mosquitos do you need to make this work?

While the malicious gene can spread exponentially in this population it does not always succeed in that goal. When the population is at an equilibrium size of about 10.000 individuals each has a chance of about 2% to survive and produce offspring. This low probability means that when we introduce too few infected individuals there is a chance that all of them will perish in the first generations due to bad luck in the lottery of life.

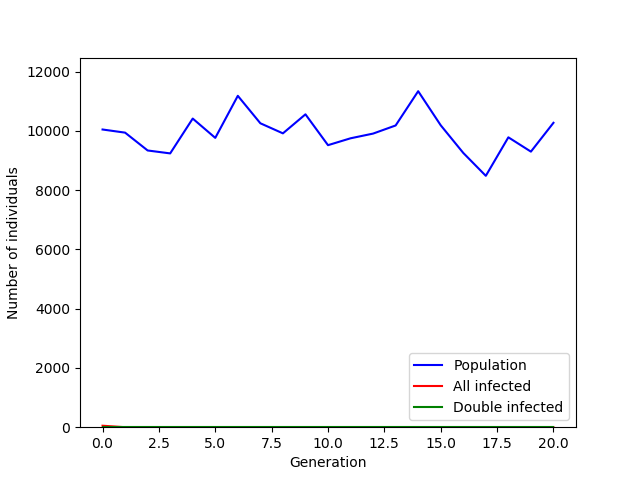
In the graph above only 50 individuals were introduced and none of them made it past the 2% survival chance in the first generation. The effect of the number of infected individuals introduced on the population’s extinction probability is something that we can once again simulate. All we have to do is create a loop over a list with different infected mosquito group sizes and run each simulation a number of times (100) so that we can calculate an average extinction probability.

if __name__ == '__main__':
    # -------------------
    # simulation settings
    # -------------------
    # While there is randomness in our simulation,
    # for a particular random seed the outcome will be the same.
    np.random.seed(1)
    # Number of infected mosquitos to introduce in the 1st generation
    infections_to_test = [1, 10, 25, 50, 75, 100, 150, 200, 300]
    # The number of simulations to run 
    # for each of the values in the list above
    n_simulations = 100
    # Number of uninfected mosquitos present in the 1st generation
    n_healthy_mosquitos = 10000

    # create an array to store per-simulation setting results
    results = np.zeros(shape=(len(infections_to_test), 2))
    
    # loop over the settings and run simulations
    for i, n_infected_mosquitos in enumerate(infections_to_test):
        n_extinct = 0
        print(n_infected_mosquitos)
        for n in range(n_simulations):
            dyn = Simulation(n_healthy=n_healthy_mosquitos,
                             n_infected=n_infected_mosquitos)
            n_extinct += dyn.main_loop(n_generations=20)[1]
        # write to the results matrix what the proportion of 
        # infected vs healthy mosquitos was + the proportion of
        # simulations where extinction took place
        results[i] = [n_infected_mosquitos / n_healthy_mosquitos,
                      n_extinct / n_simulations]
                      
    plot_meta_results(results)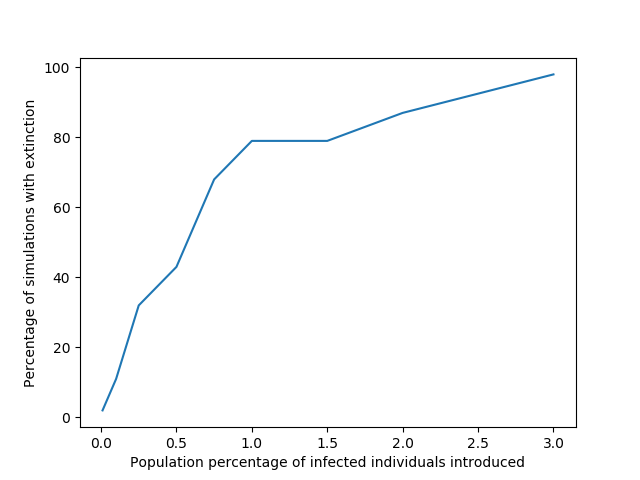

When we increase the number of individuals introduced to about 3% of the whole population (300 individuals) extinction becomes inevitable since in all 100 simulations of this situation the population went extinct. However, these numbers don’t really say that much as they depend heavily on the assumptions I’ve made regarding the population dynamics.

Is this the real life? Is this just fantasy?

Both from simulations and the lab experiments these researchers carried out it shows that giving a malicious gene a special advantage to be passed on to offspring can wipe out populations and potentially species. One big side note is that both the simulations and lab experiments concern a single, local population where all individuals are equally likely to interact with one another. In a more realistic scenario the spatial segregation of individuals and populations should be incorporated. It’s possible that the gene is so deadly that it exterminates a local population before a neighboring population can be infected which would impede a spread over large areas. In addition, some resistance to either the infertility effect of the gene or mechanism that boosts their transfer chances to the next generation could arise.

With great power comes great responsibility

Now that it seems we can wield this power, the obvious question is whether we should, both for safety, ecological, and ethical reasons. Species fit into an ecosystem through a myriad of interactions and removing one could trigger unexpected cascades when the system is insufficiently understood. Should we ban the use of a species eliminator if we had one? This is an important question up for discussion. The stakes are high but so is the prize, the power to wipe out malaria, a disease that strikes more than 200 million people each year killing more than 400.000, is very tempting indeed.

PS: Full code can be found here